まず、固有値・固有ベクトルの定義を確認する。
、、は実数とする。
ここで、上の式が成り立つとき、を固有値、を固有ベクトルという。
この式が何を意味しているのか図解する。
具体的な例として、、の場合を考える。
である。
以下にとのベクトルを示す。
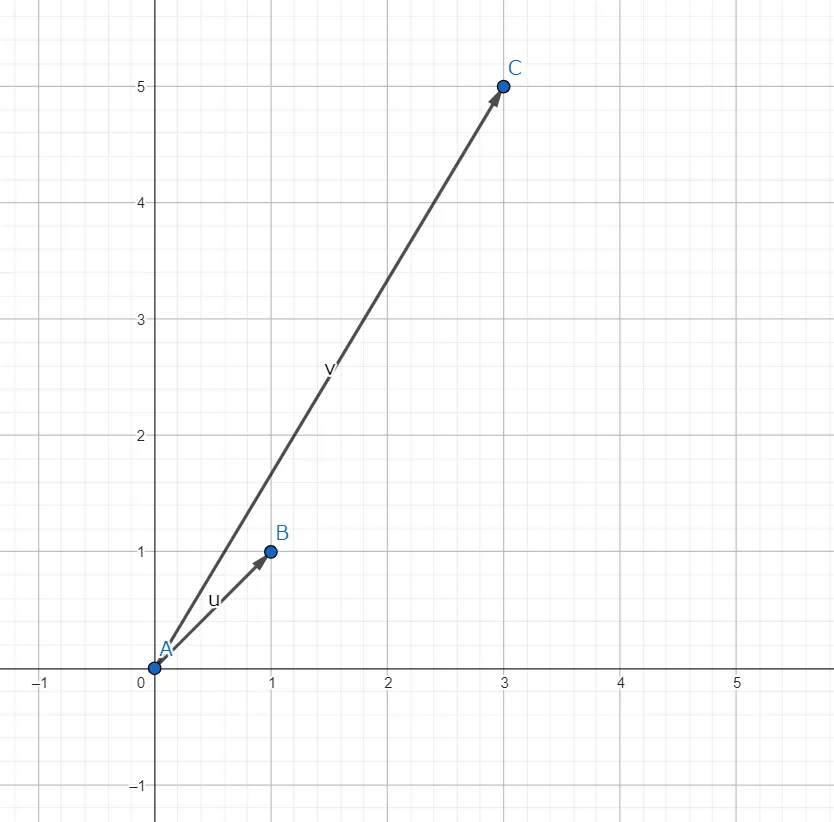
グラフにおいて、、
次に、の場合を考える。
以下にとのベクトルを示す。
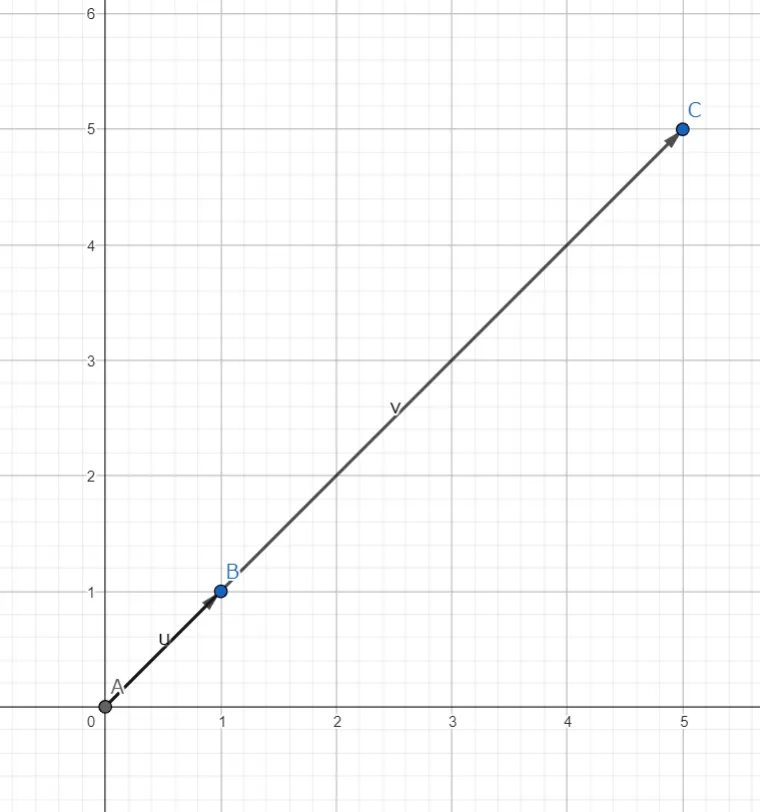
グラフにおいて、、
ここで、のときとは違い、次が成り立つ。
この時のがの固有値である。
すなわち固有値とは、あるベクトルに行列をかけたときに、元のベクトルの何倍になったかを表す値である。

